کاربرد قانون بنفورد در حسابرسی: رویکردی نوین برای تشخیص تقلب

مقدمه

در دنیای حسابرسی و بررسی مالی، یافتن راه‌های مؤثر برای تشخیص دقیق تقلب یک چالش دائمی است. با این حال، یکی از ابزارهای قدرتمند و کمتر شناخته شده‌ای که توانایی تغییر دادن به این بازی را دارد، کاربرد قانون بنفورد در حسابرسی است. این قانون، که گاهی اوقات به عنوان قانون ارقام اول نیز شناخته می‌شود، یک اصل ریاضی است که توزیع ارقام در داده‌های واقعی را به شیوه‌ای غیرانتظاری پیش‌بینی می‌کند. استفاده از این قانون در حسابرسی، به حرفه‌ای‌های مالی اجازه می‌دهد تا با استفاده از تجزیه و تحلیل آماری، انحرافات و ناهنجاری‌هایی را که ممکن است نشان‌دهنده تقلب باشد، شناسایی کنند.

مفهوم اصلی قانون بنفورد این است که در بسیاری از مجموعه‌های داده، ارقام کمتری مانند ۱ و ۲ با احتمال بیشتری نسبت به ارقام بزرگتر مانند ۸ و ۹ به عنوان رقم اول یک عدد ظاهر می‌شوند. این اصل در ابتدا ممکن است غیرمنطقی به نظر برسد، اما بررسی‌های آماری و عملی نشان داده‌اند که این الگو در انواع مختلفی از داده‌ها، از جمله اطلاعات مالی، رایج است. این الگوی منحصربه‌فرد از توزیع ارقام، قانون بنفورد را به یک ابزار ارزشمند برای حسابرسان تبدیل می‌کند، زیرا آن‌ها می‌توانند با مقایسه توزیع ارقام در داده‌های مالی با توزیع پیش‌بینی شده توسط این قانون، انحرافاتی را که ممکن است نشان‌دهنده تغییرات غیرعادی یا تقلبی باشد، شناسایی کنند.

در عمل، کاربرد قانون بنفورد در حسابرسی می‌تواند به صورت‌های مختلفی صورت گیرد. حسابرسان ممکن است از این قانون برای بررسی یک طیف گسترده‌ای از مدارک مالی، از جمله فهرست‌ها، دفترچه‌های حساب، و گزارش‌های مال

ی سالانه استفاده کنند. با تجزیه و تحلیل توزیع ارقام در این اسناد، حسابرسان می‌توانند موارد مشکوک را شناسایی کرده و تحقیقات بیشتری را برای بررسی احتمال وجود تقلب یا خطا انجام دهند.

قانون بنفورد چیست؟

قانون بنفورد، که اغلب به عنوان قانون ارقام اول نیز شناخته می‌شود، یک اصل ریاضی جالب است که در ابتدا توسط سایمون نیوکمب کشف شد و بعداً توسط فیزیکدان فرانک بنفورد به طور گسترده‌ای مطالعه و ترویج یافت. این قانون بیان می‌کند که در بسیاری از مجموعه‌های داده‌های طبیعی، ارقام کمتر با احتمال بیشتری به عنوان رقم اولیه ظاهر می‌شوند. به طور خاص، عدد ۱ به عنوان رقم اولیه در حدود ۳۰% از داده‌ها ظاهر می‌شود، در حالی که این احتمال برای عدد ۹ تنها حدود ۴.۶% است.

این پدیده به نظر می‌رسد در ابتدا غیرمنتظره و غیرقابل توجیه باشد، اما با بررسی بیشتر، مکانیسم‌های زیربنایی که باعث چنین توزیعی می‌شوند، آشکار می‌گردند. قانون بنفورد نشان‌دهنده یک توزیع لگاریتمی است و این بدان معناست که توزیع ارقام به طور مستقیم به مقیاس لگاریتمی مرتبط است. دلیل این امر این است که بسیاری از پدیده‌ها و فرایندهای طبیعی، از جمله رشد جمعیت، رشد اقتصادی و حتی فرایندهای فیزیکی مانند تشعشع رادیواکتیو، از الگوهای رشد نمایی پیروی می‌کنند که به طور طبیعی به توزیع لگاریتمی منجر می‌شود.

علاوه بر این، قانون بنفورد نه تنها در داده‌های مالی و اقتصادی بلکه در داده‌های جغرافیایی، داده‌های دموگرافیک و حتی در نتایج ورزشی و اعداد طبیعی مانند جریان رودخانه‌ها و اندازه‌های طبیعی دیگر دیده می‌شود. این اصل همچنین در مطالعات آماری گسترده، از جمله تجزیه و تحلیل داده‌های انتخاباتی و حسابداری، کاربردهای قابل توجهی دارد.

قانون بنفورد به دلیل گستردگی و قابلیت اطمینانش، ابزاری قدرتمند در تجزیه و تحلیل داده‌های بزرگ و پیچیده محسوب می‌شود. به ویژه، حسابرسان و محققان مالی از این قانون برای شناسایی ناهنجاری‌ها و تقلب‌های احتمالی در داده‌ها استفاده می‌کنند. هر گونه انحراف قابل توجه از توزیع انتظاری قانون بنفورد ممکن است نشان‌دهنده دستکاری یا خطای مالی باشد که نیازمند بررسی بیشتر است.

قانون بنفورد تک رقمی و دو رقمی

قانون بنفورد تک رقمی بیان می‌کند که در بسیاری از مجموعه‌های داده‌های طبیعی و واقعی، احتمال ظاهر شدن ارقام کمتر به عنوان رقم اولیه بیشتر است. به عنوان مثال، در یک مجموعه داده طبیعی، رقم ۱ به عنوان رقم اولیه با احتمال حدود ۳۰% ظاهر می‌شود، در حالی که رقم ۹ فقط با احتمال حدود ۴.۶% به عنوان رقم اولیه ظاهر می‌شود. این توزیع احتمالاتی که توسط قانون بنفورد تک رقمی پیش‌بینی می‌شود، نشان می‌دهد که داده‌ها از یک الگوی خاص پیروی می‌کنند که در بسیاری از سیستم‌ها و پدیده‌های طبیعی یافت می‌شود.

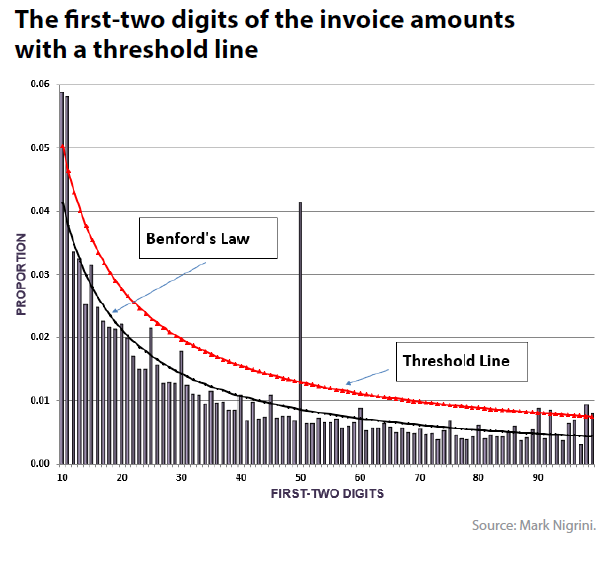
در مقابل، قانون بنفورد دو رقمی به توزیع احتمالاتی ارقام دوم در یک مجموعه داده‌های طبیعی می‌پردازد و این امر پیچیدگی بیشتری را به همراه دارد. تجزیه و تحلیل دو رقمی نه تنها به ارقام اولیه بلکه به جفت ارقام اولیه و دومیه نیز توجه دارد. برای مثال، در توزیع دو رقمی، ترکیبات خاصی از ارقام اول و دوم با احتمالات متفاوتی ظاهر می‌شوند که این احتمالات بر اساس لگاریتم‌های طبیعی تعیین می‌گردند. این بدان معناست که تجزیه و تحلیل دو رقمی می‌تواند الگوهای پیچیده‌تری را در داده‌ها شناسایی کند و در نتیجه اطلاعات بیشتری در مورد ساختار و خصوصیات داده‌ها ارائه دهد.

تفاوت اصلی بین قانون بنفورد تک رقمی و دو رقمی در عمق و دقت تجزیه و تحلیل قرار دارد. در حالی که تجزیه و تحلیل تک رقمی به سادگی به رقم اولیه توجه دارد و یک نگاه کلی از توزیع داده‌ها ارائه می‌دهد، تجزیه و تحلیل دو رقمی با بررسی ترکیبات ارقام اول و دوم، به جزئیات بیشتری می‌پردازد و می‌تواند ناهنجاری‌ها و الگوهای پنهان را با دقت بیشتری آشکار سازد. این تجزیه و تحلیل دقیق‌تر از قانون بنفورد دو رقمی، ابزاری قوی‌تر در شناسایی تقلب یا اشتباهات احتمالی در داده‌های مالی یا سایر مجموعه‌های داده‌های بزرگ محسوب می‌شود.

تعداد رکوردهای موثر در قانون بنفورد

در استفاده از قانون بنفورد برای نمونه‌گیری در حسابرسی، انتخاب اندازه‌ی مناسب نمونه اهمیت بالایی دارد. این قانون می‌تواند به حسابرسان کمک کند تا داده‌هایی را که از یک توزیع طبیعی پیروی نمی‌کنند شناسایی کرده و بررسی نمایند. به طور کلی، برای اینکه یک تحلیل بر اساس قانون بنفورد معتبر باشد، باید داده‌های کافی وجود داشته باشد. اگرچه تعداد دقیق رکوردها ممکن است بر اساس شرایط خاص هر مجموعه داده‌ای متفاوت باشد، اما اصول کلی وجود دارد که می‌تواند راهنمایی کند.

برای اعمال قانون بنفورد به طور مؤثر، توصیه می‌شود که از نمونه‌ای با حداقل ۱۰۰ مشاهده استفاده شود. این امر از آنجا نشأت می‌گیرد که با افزایش تعداد داده‌ها، دقت تحلیل بر اساس قانون بنفورد نیز بهبود می‌یابد. استفاده از داده‌های کامل یک سال مالی می‌تواند ایده‌آل باشد، اما در صورتی که تعداد آیتم‌ها زیاد باشد، می‌توان از نمونه‌های کوچکتر نیز استفاده کرد. این امر به ویژه مفید است زمانی که محدودیت‌های زمانی یا منابع وجود دارد که از بررسی کل داده‌ها جلوگیری می‌کند.

علاوه بر این، مهم است که حسابرسان هنگام انتخاب داده‌ها برای نمونه‌گیری به ویژگی‌های خاص مجموعه داده‌ها توجه کنند. قانون بنفورد بهترین عملکرد را در مجموعه داده‌هایی دارد که از چندین مرتبه اندازه متفاوت پیروی می‌کنند و در آن‌ها رشد به صورت نمایی رخ می‌دهد. این شامل داده‌هایی می‌شود که در طول یک دوره زمانی چندین برابر می‌شوند. به این ترتیب، قانون بنفورد می‌تواند به عنوان ابزاری برای شناسایی انحرافات یا الگوهای غیرعادی در داده‌ها عمل کند که ممکن است نیاز به بررسی بیشتر داشته باشند

کاربرد قانون بنفورد در حسابرسی

کاربرد قانون بنفورد در حسابرسی به عنوان یک ابزار مؤثر و قدرتمند برای شناسایی تقلب و ناهنجاری‌های مالی شناخته شده است. حسابرسان از این قانون برای بررسی و تحلیل داده‌های مالی استفاده می‌کنند تا بتوانند هرگونه انحراف یا ناسازگاری از الگوهای انتظاری را شناسایی کنند. به طور خاص، وقتی ارقام در گزارش‌های مالی از توزیع انتظاری قانون بنفورد دور باشند، می‌تواند نشانه‌ای از دستکاری یا خطای محاسباتی باشد.

یکی از مزایای اصلی استفاده از قانون بنفورد در حسابرسی، توانایی آن در پوشش دادن به یک محدوده وسیع از داده‌ها و بررسی مقدماتی آن‌ها بدون نیاز به تحلیل‌های عمیق و زمان‌بر است. این امر حسابرسان را قادر می‌سازد تا به سرعت و با کارایی بالا به بررسی اولیه داده‌ها بپردازند و مناطقی که ممکن است شامل خطا یا تقلب باشند را شناسایی کنند.

علاوه بر این، قانون بنفورد می‌تواند در شناسایی نوع خاصی از تقلب‌ها مانند تحریف درآمدها، پنهان کردن بدهی‌ها یا سایر انواع دستکاری‌های مالی مؤثر باشد. این امر به‌ویژه در مواردی که افراد سعی در جلوگیری از شناسایی فعالیت‌های مشکوک با استفاده از روش‌های معمول دارند، کاربرد دارد.

در مواردی که حسابرسان با حجم عظیمی از داده‌های مالی روبرو هستند، استفاده از قانون بنفورد به عنوان ابزاری برای اولویت‌بندی بررسی‌ها و تمرکز بر روی مواردی که بیشترین احتمال تقلب یا خطا را دارند، مفید است. این امر منجر به بهره‌وری بیشتر در فرآیند حسابرسی و کاهش زمان مورد نیاز برای شناسایی موارد مشکوک می‌شود.

نهایتاً، استفاده از قانون بنفورد در حسابرسی نه تنها به شناسایی تقلب کمک می‌کند بلکه می‌تواند به عنوان یک ابزار پیشگیرانه عمل کند. دانش و آگاهی از اینکه حسابرسان ممکن است از قانون بنفورد برای شناسایی تقلب‌ها استفاده کنند، می‌تواند افراد را از ارتکاب تقلب باز دارد.

اعمال قانون بنفورد در حسابرسی با کمک حسابرسیار

نرم‌افزار حسابرسی حسابرسیار، با تکیه بر تجربه‌ای ۱۷ ساله و همکاری با حدود ۳۵ موسسه حسابرسی رسمی در ایران، ابزاری قدرتمند و جامع برای انجام حسابرسی‌های مالی محسوب می‌شود. این نرم‌افزار در طول سال‌ها با دریافت بازخوردها و عملکردها در شرکت‌ها و سازمان‌ها به مرحله‌ای از رشد و تکامل نزدیک شده و نسخه ۸ آن در حال حاضر قابل ارائه است .

یکی از کاربردهای بارز حسابرسیار، قابلیت آن در تسهیل فرآیند حسابرسی و کاهش هزینه‌ها و خطاهای انسانی است. با استفاده از این نرم‌افزار، حسابرسان می‌توانند به اطلاعات کاملی از حساب‌ها و اشکالات موجود در داده‌های مالی دسترسی داشته باشند و به صورت مؤثری از وابستگی به سیستم مالی واحد مربوطه بی‌نیاز شوند.

استفاده از قانون بنفورد در نرم افزار حسابرسی حسابرسیار می‌تواند بخش مهمی از فرآیند نمونه‌گیری و رسیدگی به حساب‌ها را تسهیل کند. این قانون به حسابرسان این امکان را می‌دهد تا با شناسایی الگوهای غیرعادی در داده‌های مالی، به سرعت مناطقی که ممکن است نیاز به بررسی بیشتر داشته باشند را شناسایی کنند. در نرم‌افزار حسابرسیار، این فرآیند می‌تواند به صورت اتوماتیک انجام شود، که به حسابرسان اجازه می‌دهد تا با استفاده از ابزارها و قابلیت‌های تحلیلی نرم‌افزار، رویه‌های حسابرسی خود را بهینه‌سازی کنند.

به عنوان مثال، در بخش حسابرسی نرم‌افزار، امکاناتی مانند تهیه کاربرگ‌ها، سیستم عطف‌گذاری هوشمند، و انتخاب نمونه‌های مؤثر برای رسیدگی فراهم می‌شود. با استفاده از قانون بنفورد، می‌توان ارقامی را که با احتمال بیشتری نشان‌دهنده ناسازگاری یا احتمال تقلب هستند، شناسایی کرد. در نتیجه، حسابرسان می‌توانند تمرکز خود را بر روی این مناطق افزایش داده و از زمان و منابع خود به طور مؤثرتری استفاده کنند.

علاوه بر این، قابلیت‌های گزارش‌دهی و تحلیلی نرم‌افزار حسابرسیار به حسابرسان امکان می‌دهد تا نتایج حاصل از نمونه‌گیری و رسیدگی‌های خود را به صورت واضح و دقیق مستندسازی کنند. این امر نه تنها فرآیند حسابرسی را شفاف‌تر و قابل پیگیری‌تر می‌کند، بلکه به افزایش اعتبار و اطمینان از نتایج حاصل از حسابرسی نیز کمک می‌کند.

بنابراین، استفاده از قانون بنفورد در نرم‌افزار حسابرسیار، از طریق تسهیل فرآیند نمونه‌گیری و بهبود دقت و کارایی فرآیندهای حسابرسی، مزایای قابل توجهی را برای حسابرسان و مؤسسات حسابرسی به همراه می‌آورد. این نه تنها به کاهش خطاها و افزایش کیفیت گزارش‌دهی کمک می‌کند،با استفاده از قانون بنفورد در نرم‌افزار حسابرسی حسابرسیار، حسابرسان قادر به بهینه‌سازی فرآیند نمونه‌گیری و تمرکز بر روی تراکنش‌هایی هستند که بیشترین احتمال برای دارا بودن ناسازگاری‌ها یا نشانه‌های تقلب را دارند. این قابلیت، که در بخش‌های مختلف نرم‌افزار مانند تهیه کاربرگ‌ها، سیستم عطف‌گذاری هوشمند، و انتخاب نمونه‌های مؤثر برای رسیدگی مورد استفاده قرار می‌گیرد، به حسابرسان امکان می‌دهد تا روند حسابرسی را به طور کارآمد و دقیق‌تری مدیریت کنند.

نتیجه‌گیری

قانون بنفورد، با تکیه بر تجزیه و تحلیل ریاضی و آماری داده‌ها، ابزاری قدرتمند در اختیار حسابرسان قرار می‌دهد تا به شناسایی تقلب و ناهنجاری‌ها در داده‌های مالی بپردازند. استفاده از این قانون به‌عنوان بخشی از فرایند حسابرسی، می‌تواند به افزایش شفافیت و دقت در گزارش‌های مالی کمک کند و اعتماد ذینفعان را تقویت نماید.